延伸阅读-浮点数二进制存储
1. 浮点数的二进制存储
浮点数相对比较复杂:它由三部分组成:符号位,指数位,小数部分
例如对于float来讲:
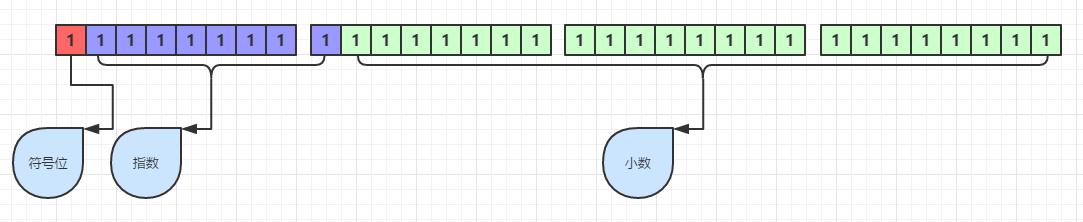
符号位1位,以s表示,取值 (-1)^s
指数部分8位,以E表示,取值 -126~127,存储时在真正指数值的基础上+127
小数部分23位,以M表示,1<=M<2 。
采用科学计数法表示的二进制小数,因为M总是1.xxxx,所以保存时只存储小数部分,例如1.01只存储小数部分的01,整数部分读取时再加上,这样的目的可以多存储一位数,即24位。
比如:9.5 的二进制为1001.1,采用科学计数法后为1.0011 * 2^3
符号位和小数比较简单
指数部分存储规则:
0000 0011 (十进制3)
0111 1111 (十进制127)
+ -------------------------
1000 0010 (十进制-126)
最终的存储格式为:
| 符号位 | 指数 | 小数 |
|---|---|---|
| 0 | 1000 0010 | 001 1000 0000 0000 0000 0000 |
2. 浮点数精度问题
以小数部分的精度为例:刚才分析过小数部分能够表示的最大范围是24位,换算成十进制就是2^24=16777216
看看这个数值前后在存储时有什么问题:
| 实际数 float表示的浮点数 | 二进制存储 |
|---|---|
| 16777211 1.6777211E7 | 0100 1011 0111 1111 1111 1111 1111 1011 |
| 16777212 1.6777212E7 | 0100 1011 0111 1111 1111 1111 1111 1100 |
| 16777213 1.6777213E7 | 0100 1011 0111 1111 1111 1111 1111 1101 |
| 16777214 1.6777214E7 | 0100 1011 0111 1111 1111 1111 1111 1110 |
| 16777215 1.6777215E7 | 0100 1011 0111 1111 1111 1111 1111 1111 |
| 16777216 1.6777216E7 | 0100 1011 1000 0000 0000 0000 0000 0000 |
| 16777217 1.6777216E7 | 0100 1011 1000 0000 0000 0000 0000 0000 |
| 16777218 1.6777218E7 | 0100 1011 1000 0000 0000 0000 0000 0001 |
| 16777219 1.677722E7 | 0100 1011 1000 0000 0000 0000 0000 0010 |
| 16777220 1.677722E7 | 0100 1011 1000 0000 0000 0000 0000 0010 |
| 16777221 1.677722E7 | 0100 1011 1000 0000 0000 0000 0000 0010 |
可以看到16777215 之前的数据没有问题,注意到 16777216 与 16777217在存储时值已经相同;类似的,16777219、16777220、16777221三个数在存储时也是相同的。
换句话说,这时候计算机已经无法区分它们了,可以验证:
System.out.println(16777216f == 16777217f); // true
System.out.println(16777220f == 16777219f); // true
System.out.println(16777220f == 16777221f); // true
结论:float的小数部分只能够精确到2^23,也就是小于16777216 的数字能够保证小数点后7位都是有效的,大于等于它的数只能保证小数点后6位是有效的。
3. 浮点数的运算误差
前面的精度,是指浮点数在存储时发生的。此外浮点数在运算时也会有一定问题,下面来详细分析。
| 运算 | 结果 |
|---|---|
| 2.0f-1.5f | 0.5 |
| 2.0f-1.4f | 0.6 |
| 2.0f-1.3f | 0.70000005 |
| 2.0f-1.2f | 0.79999995 |
| 2.0f-1.1f | 0.9 |
| 12.0f-11.9f | 0.10000038 |
看到以上结果,霎时间感觉不好了:连简单的小数减法都算不对!
来分析一下过程吧,主要分析小数部分:
2.0f-1.5f
0100 0000 0000 0000 0000 0000 0000 0000 (2.0)
0011 1111 1100 0000 0000 0000 0000 0000 (1.5)
提取小数部分,并对齐
1.00000000000000000000000 (2.0 从存储区域取后23位,前面补一个1.0)
0.110000000000000000000000 (1.5 从存储区域取后23位,前面补一个1.0,小数点要左移一位,保证与2.0对齐)
减法
0.010000000000000000000000
采用1.xxxx科学计数法表示,小数保留23位(小数点向右移了2位,补了一个0)
1.000 0000 0000 0000 0000 0000
对比真正0.5
0011 1111 0000 0000 0000 0000 0000 0000 (真的0.5 )
xxxx xxxx x000 0000 0000 0000 0000 0000 (我们的2.0-1.5)
发现它们的小数部分都是一致的,没有误差
2.0f-1.4f
0100 0000 0000 0000 0000 0000 0000 0000 (2.0)
0011 1111 1011 0011 0011 0011 0011 0011 (1.4)
提取小数部分,并对齐
1.00000000000000000000000 (2.0 从存储区域取后23位,前面补一个1.0)
0.101100110011001100110011 (1.4 从存储区域取后23位,前面补一个1.0,小数点要左移一位,保证与2.0对齐)
减法
0.010011001100110011001101
采用1.xxxx科学计数法表示,小数保留23位(小数点向右移了2位,补了一个0)
1.001 1001 1001 1001 1001 1010
对比真正0.6
0011 1111 0001 1001 1001 1001 1001 1010 (真的0.6 )
xxxx xxxx x001 1001 1001 1001 1001 1010 (我们的2.0-1.4)
发现它们的小数部分都是一致的,没有误差
2.0f-1.3f
0100 0000 0000 0000 0000 0000 0000 0000 (2.0)
0011 1111 1010 0110 0110 0110 0110 0110 (1.3)
提取小数部分,并对齐
1.00000000000000000000000 (2.0 从存储区域取后23位,前面补一个1.0)
0.101001100110011001100110 (1.3 从存储区域取后23位,前面补一个1.0,小数点要左移一位,保证与2.0对齐)
减法
0.010110011001100110011001
采用1.xxxx科学计数法表示,小数保留23位(小数点向右移了2位,补了一个0)
1.011 0011 0011 0011 0011 0010
对比真正0.7
0011 1111 0011 0011 0011 0011 0011 0011 (真的0.7 )
xxxx xxxx x011 0011 0011 0011 0011 0010 (我们的2.0-1.3)
发现最后一位不一样,失之毫厘,谬以千里,问题就出在保留23位小数结果时,在最末尾补0,但不是所有情况补0都正确!
2.0f-1.2f
0100 0000 0000 0000 0000 0000 0000 0000 (2.0)
0011 1111 1001 1001 1001 1001 1001 1010 (1.2)
提取小数部分,并对齐
1.00000000000000000000000 (2.0 从存储区域取后23位,前面补一个1.0)
0.100110011001100110011010 (1.2 从存储区域取后23位,前面补一个1.0,小数点要左移一位,保证与2.0对齐)
减法
0.011001100110011001100110
采用1.xxxx科学计数法表示,小数保留23位(小数点向右移了2位,补了一个0)
1.100 1100 1100 1100 1100 1100
对比真正0.8
0011 1111 0100 1100 1100 1100 1100 1101 (真的0.8 )
xxxx xxxx x100 1100 1100 1100 1100 1100 (我们的2.0-1.2)
发现最后一位不一样,失之毫厘,谬以千里,问题就出在保留23位小数结果时,在最末尾补0,但不是所有情况补0都正确!
12.0f-11.9f
0100 0001 0100 0000 0000 0000 0000 0000 (12.0)
0100 0001 0011 1110 0110 0110 0110 0110 (11.9)
提取小数部分,并对齐
1.10000000000000000000000 (2.0 从存储区域取后23位,前面补一个1.0)
1.01111100110011001100110 (1.2 从存储区域取后23位,前面补一个1.0)
减法
0.00000011001100110011010
采用1.xxxx科学计数法表示,小数保留23位(小数点向左移了7位,补了7个0)
1.100 1100 1100 1101 0000 0000
对比真正0.1
0011 1101 1100 1100 1100 1100 1100 1101 (真的0.1 )
xxxx xxxx x100 1100 1100 1101 0000 0000 (我们的12.0-11.9)
这回差的有点大,因为我们补了7个0
附:将float中的每个bit打印出来的工具方法:
private static void print(float a) {
String s = String.format("%32s", Integer.toBinaryString(Float.floatToIntBits(a))).replaceAll("\\s","0");
StringBuilder sb = new StringBuilder(32+8);
for(int i = 0; i<s.length();i++) {
sb.append(s.charAt(i));
if((i+1) % 4 == 0){
sb.append(" ");
}
}
System.out.println(sb.toString());
}