延伸阅读-整数二进制存储
首先明白一点,计算机里只能保存0或1,即二进制的形式,无论是整数、浮点数、字符、还是图片,到了计算机中,都得保存为0或1.
1. 整数的二进制存储
整数指byte, short, int, long这四种类型。以byte为例,它长度为一个字节,即8位(bit),最多能够保存8个0或者1
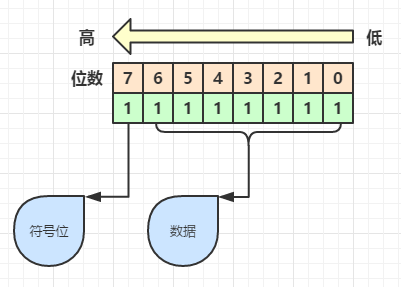
上图表示这一个byte中保存了8个1,它代表什么数字呢?
先看低7位,它们每一位的1换算成十进制数就是2^n 次方。
例如:
第0位的1换算成十进制就是 2^0 = 1
第1位的1换算成十进制就是 2^1 = 2
第2位的1换算成十进制就是 2^2 = 4
第3位的1换算成十进制就是 2^3 = 8
... ...
简单点理解高位的一个1就是稍低一位的两倍:100 是10的两倍(一个顶2个),就像十进制的100 相比10 来说,第2位的1是第1位的1的10倍(一个顶10个)
初步结论是,低7位是:
1111111 = 2^6+2^5+2^4+2^3+2^2+2^1+2^0=127
最高位的1,很多教程中都解释为符号位:1代表负数、0代表正数,这么理解可以。
但我可以给一个更好的解释,最高位的1仍可以按上述规则来换算,刚才的例子中,它就是:
2^7 = 128
但要记得给它加个负号,结果是 -128
最终结论是:
最高位 + 低7位 = -128 + 127 = -1
要再深究的话,需要看看微机原理,CPU做运算时只有加法器,没有什么减法器,之所以这么设计最高位,是为了方便加法计算,举个例子:
1000 0001 (十进制 -127)
0111 1111 (十进制 127)
+ -------------------------
0000 0000 (十进制 0 )
第一个数的低7位是1,第二个数的低7位是127,加起来是128和最高位的-128 正好抵消成0(溢出)
注意:前提是,运算的结果不能超过其存储范围(-128~127)
2. 负数存储的艺术
以字节为例:
首先介绍一个特殊的数字,前面已经见过127 二进制表示为 0111 1111.
为什么说它特殊呢?考虑几个7位二进制(127以内)的正整数求和,请看下面几个例子:
| a | b | 和 | 备注 |
|---|---|---|---|
| 000 0000 | 111 1111 | 111 1111 | 0 + 127 = 127 |
| 111 0000 | 000 1111 | 111 1111 | 112 + 15 = 127 |
| 101 0000 | 010 1111 | 111 1111 | 80 + 47 = 127 |
| ... | ... | 111 1111 | ... + ... = 127 |
发现规律:只要它们最后的和为127,a和b的关系恰巧是逐位取反,以后a和b可以称对方为反码。这个挺好理解,127就是二进制的7个1,把这7个1随便组合来,组合去,结果一定还是127。
注意:a和b的十进制是多少其实并不重要
好,下面我想存储一个-15,如何存储呢?
-15 = (-128+128) -15
= (-128) + (128-15)
= (-128) + (1+127-15)
= (-128) + (1+15的反码)
下面我们不用做减法运算了,记得-128是 1000 0000 喔,合在一起,结果是:
1000 0000 (-128)
0000 0001 (1)
0111 0000 (15的反码112)
+ -------------------------
1111 0001 (-15)
最后的结果,计算机教程里把它叫做15的补码:所有位取反+1,结论比我的简单,但失去推导过程的话,比较难理解。
以后它再跟其它数做运算时,也可以避免减法运算,比如:-15+16
1111 0001 (-15)
0001 0000 (16)
+ -------------------------
0000 0001 (1)
最后进位得到的128正好和最高为的-128抵消(溢出)了。